深层神经网络(Deep Neural Network)
深度学习(Deep Learning)和深层神经网络(DNN)
现在很火的深度学习的概念,其实在实际中基本上可以认为是深层神经网络的代名词。那么为什么要叫“深层”呢?与上一篇笔记中的神经网络又有什么区别呢?
上一篇笔记中的神经网络,其实使用的是线性模型:y = Σxiwi + b(偏置),任意线性模型组合仍为线性→单层←→多层,线性模型仅可解决线性可分问题,那么如何去线性化(全连接非线性问题),这时候我们就要引入这篇笔记的主角——深层神经网络。
深层神经网络有两个非常重要的特性——①非线性、②多层,下面一一阐述
①非线性
- 相对于以往的神经网络,由于没有使用激活函数,构造出来的函数往往形如:w1x1+w2x2+…+wnxn + b = 0,很显然这种函数只能模拟线性分割。即只能通过直线来划分,一旦分割面是一个圆形,通过这种方式只能尽可能的得到一个多棱角保卫面,而不能拟合成圆形,存在很大的误差。
- 细想一下,如果我们换一种权重作用方式,比如将w1x1换为x1^w1 或者 w1*e^x1,很显然这种指数函数作用的结果是一种弯曲状态,就能够拟合上面所说的圆形。但是,目前我们采用的方式是直接在输出层外加上一层激活函数(弯曲函数),就能够实现这种方式(不同的函数作用效果也不一样)。通过激活函数(NN去线性化)有3种:
- ①tf.nn.relu();
- ②tf.nn.sigmoid();
- ③tf.nn.tanh();
②多层
- 还是相对于之前的神经网络,由于之前的神经网络没有隐藏层,相当于只有一层权重作用在输入变量上面,这样,w1x1+w2x2+…+wnxn + b = 0函数作用下,无论是几维空间,输出的结果总是为一条直线。
- 考虑下简单地二维空间,比如进行异或运算。这种方式显然不能够通过一条直线就能够分成两类。再到多维,那将更不可能,一条直线只能分两类,多个类就无法实行。
- 现在我们想想,既然一层能画一条直线,那我多画几条直线,然后将这两条直线组合一下不就可以了吗?确实是这样,比如进行异或运算,加上一个隐藏层,隐藏层节点为4,这输入到这四个节点的都负责自己的一部分划分,分别划分四个点区域,这样,输出处理时将这四个区域进行组合,就是整个完整的区域。
- 多个隐藏层逐层抽取更高层特征(高层次特征抽取)——解决异或可分,综上,深层神经网络实际上有组合特征提取的特性,这个特性对于解决不易提取特征向量的问题(比如图像识别、语义识别等)有很大帮助。
多层 + 非线性
深度学习应深层数且非线性,可解决:
- 回归:预测具体的数值
- 分类:分入事先定义好的类,并以概率形式(当输出通过softmax()函数时可满足)输出
深层神经网络的度量
- NN大小:多用待优化的参数个数表示
- 层数:从隐藏层到输出层
- 总参数:总W+总b
损失函数
损失函数度量了训练结果和实际结果之间的一种差别,通过这种差别大小来调整神经网络的参数,以此达到优化神经网络的目的。
经典损失函数
分类问题的损失函数一般使用交叉熵配合softmax回归;回归问题由于是连续的,一般只有一个输出节点,所以损失函数使用的是均方误差MSE。
- 损失函数的计算方式有很多,不同的领域都有各自最优化的方式。经典损失函数就是分类问题和回归问题经常使用到的损失函数。
- 经典损失函数是一种对训练输出值和实际值相似度的度量,值越小,相似度越大,更准确的解释:经典损失函数(交叉熵)刻画了两个分布概率之间的距离。
- 公式:H(p,q)=−∑p(x)logq(x),这里的p代表真确答案,q代表预测值
显然∑q(x)=1,即概率和等于1。因此,我们需要将输出转化为概率类型。一般而言,我们可以直接计算输出值在整个输出中出现的概率作为计算值,这里我们使用了softmax函数。 - softmax回归函数,是将神经网络的输出结果变成概率分布,softmax(yi)=yi’=e^yi/∑e^yj
- 均方误差函数:MSE(y,y′)=∑(yi−y’i)^2/n
- 其他损失函数:不同问题不同对待
自定义损失函数
TensorFlow不仅支持经典的损失函数,还可以优化任意的自定义损失函数。可以通过以下代码来实现这个损失函数:
#在TensorFlow1.0.0以上版本中select改成了where,因此低版本请使用tf.select函数
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), loss_more * (y-y_), loss_less*(y_-y)))
神经网络优化
梯度下降算法
- 梯度的反方向是函数下降最快的方向,通过这个方式计算,就能够使得函数向着极小值方向迭代,从而达到训练的目的。
- 学习率:通过在梯度下降值上加上一个学习率权重,来控制下降的幅度/步长,即控制下降速度的快慢。
- 学习率的取值:η大了震荡不收敛(1)
- η小了速度慢
- η常用指数衰减
learing_rate = strat_rate * decay_rate ^ (global-step/decay_steps)
其中global-step:运行了几次Batch;
decay_steps:每轮学习步数 = 总样本/Batch。
- 几个缺点:
1.只是局部最优解不是全局最优解
2.计算时间长-由于损失函数计算的是所有训练数据上的损失和,所以计算量大
3.为了加快梯度下降,我们可以采用随机梯度下降或者小批量随机下降
进一步的优化
- 学习率的优化:在训练初期,差别往往很大,所以这个时候学习率相对较大能够加快训练的速度;但是随着训练的深入,差别减小,为了防止下降跨度太大导致越界,需要降低学习率;这个时候就可以对学习率进行指数衰减。
- 正则化缓解过拟合:正则化在损失函数中引入了模型复杂度指标,利用给w加权重,弱化了训练数据的噪声
- 过拟合问题:样本不足、样本有噪声、模型结构过于复杂都将导致模型过拟合。
- 正则化:为了避免模型复杂导致的过拟合,我们引入了一个思想,即在损失函数中引入/加入衡量模型复杂度的指标,r*R(w),r为正则化系数,R(w)为描述的是模型参数的大小,通过之中方式限制模型参数的大小来限制模型的复杂度。L1、L2正则化
- 滑动平均模型使模型泛化性更好(在测试数据时更优),使得模型更加健壮,即更加稳定
- 方法:给参数加了影子,参数变化,影子慢慢追随
影子 = 衰减率 x 影子 + (1-衰减率) x 参数 - 这种模型通过在损失函数中加入一个衰减率decay来,缓冲模型参数变量的变化程度,即不让他变化过大,能走10步的,只让它走一步。
- 衰减变量:上面这种方式训练速度有点慢,为了让训练初期快,比如走9步,有引入了参数衰减变量,通过训练次数来控制滑动平均的步长大小,越到后期步长越慢。
- 方法:给参数加了影子,参数变化,影子慢慢追随
下面给出一个带所有优化算法的例程(损失函数有无正则项的区别)以进行进一步比较:
#coding:utf-8
#1. 生成模拟数据集。
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
data = []
label = []
np.random.seed(0)
# 以原点为圆心,半径为1的圆把散点划分成红蓝两部分,并加入随机噪音。
for i in range(150):
x1 = np.random.uniform(-1,1)
x2 = np.random.uniform(0,2)
if x1**2 + x2**2 <= 1:
data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
label.append(0)
else:
data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
label.append(1)
data = np.hstack(data).reshape(-1,2)
label = np.hstack(label)#.reshape(-1, 1)
plt.scatter(data[:,0], data[:,1], c=label,
cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()
nlabel = np.hstack(label).reshape(-1, 1)
#2. 定义一个获取权重,并自动加入正则项到损失的函数。
def get_weight(shape, lambda1):
var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var))
return var
#3. 定义神经网络。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
sample_size = len(data)
# 每层节点的个数
layer_dimension = [2,10,5,3,1]
n_layers = len(layer_dimension)
cur_layer = x
in_dimension = layer_dimension[0]
# 循环生成网络结构
for i in range(1, n_layers):
out_dimension = layer_dimension[i]
weight = get_weight([in_dimension, out_dimension], 0.003)
bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
cur_layer = tf.nn.elu(tf.matmul(cur_layer, weight) + bias)
in_dimension = layer_dimension[i]
y= cur_layer
# 损失函数的定义。
mse_loss = tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size
tf.add_to_collection('losses', mse_loss)
loss = tf.add_n(tf.get_collection('losses'))
#4. 训练不带正则项的损失函数mse_loss。
# 定义训练的目标函数mse_loss,训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS = 40000
with tf.Session() as sess:
tf.initialize_all_variables().run()
for i in range(TRAINING_STEPS):
sess.run(train_op, feed_dict={x: data, y_: nlabel})
if i % 2000 == 0:
print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: nlabel})))
# 画出训练后的分割曲线
xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = sess.run(y, feed_dict={x:grid})
probs = probs.reshape(xx.shape)
plt.scatter(data[:,0], data[:,1], c=label,
cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()
"""
After 0 steps, mse_loss: 2.315934
After 2000 steps, mse_loss: 0.054761
After 4000 steps, mse_loss: 0.047252
After 6000 steps, mse_loss: 0.029857
After 8000 steps, mse_loss: 0.026388
After 10000 steps, mse_loss: 0.024671
After 12000 steps, mse_loss: 0.023310
After 14000 steps, mse_loss: 0.021284
After 16000 steps, mse_loss: 0.019408
After 18000 steps, mse_loss: 0.017947
After 20000 steps, mse_loss: 0.016683
After 22000 steps, mse_loss: 0.015700
After 24000 steps, mse_loss: 0.014854
After 26000 steps, mse_loss: 0.014021
After 28000 steps, mse_loss: 0.013597
After 30000 steps, mse_loss: 0.013161
After 32000 steps, mse_loss: 0.012915
After 34000 steps, mse_loss: 0.012671
After 36000 steps, mse_loss: 0.012465
After 38000 steps, mse_loss: 0.012251
"""
#5. 训练带正则项的损失函数loss。
# 定义训练的目标函数loss,训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS = 40000
with tf.Session() as sess:
tf.initialize_all_variables().run()
for i in range(TRAINING_STEPS):
sess.run(train_op, feed_dict={x: data, y_: nlabel})
if i % 2000 == 0:
print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data, y_:nlabel})))
# 画出训练后的分割曲线
xx, yy = np.mgrid[-1:1:.01, 0:2:.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = sess.run(y, feed_dict={x:grid})
print(probs)
probs = probs.reshape(xx.shape)
plt.scatter(data[:,0], data[:,1], c=label,
cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()
"""
After 0 steps, loss: 2.468601
After 2000 steps, loss: 0.111190
After 4000 steps, loss: 0.079666
After 6000 steps, loss: 0.066808
After 8000 steps, loss: 0.060114
After 10000 steps, loss: 0.058860
After 12000 steps, loss: 0.058358
After 14000 steps, loss: 0.058301
After 16000 steps, loss: 0.058279
After 18000 steps, loss: 0.058266
After 20000 steps, loss: 0.058260
After 22000 steps, loss: 0.058255
After 24000 steps, loss: 0.058243
After 26000 steps, loss: 0.058225
After 28000 steps, loss: 0.058208
After 30000 steps, loss: 0.058196
After 32000 steps, loss: 0.058187
After 34000 steps, loss: 0.058181
After 36000 steps, loss: 0.058177
After 38000 steps, loss: 0.058174
"""
运行结果:
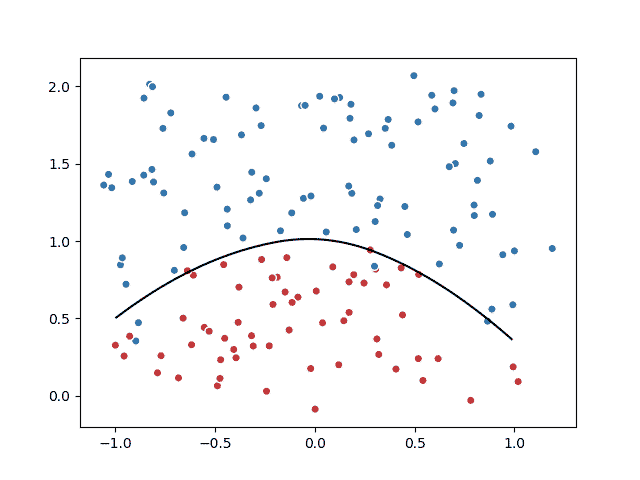
- 以原点为圆心,半径为1的圆把散点划分成红蓝两部分,并加入随机噪音:
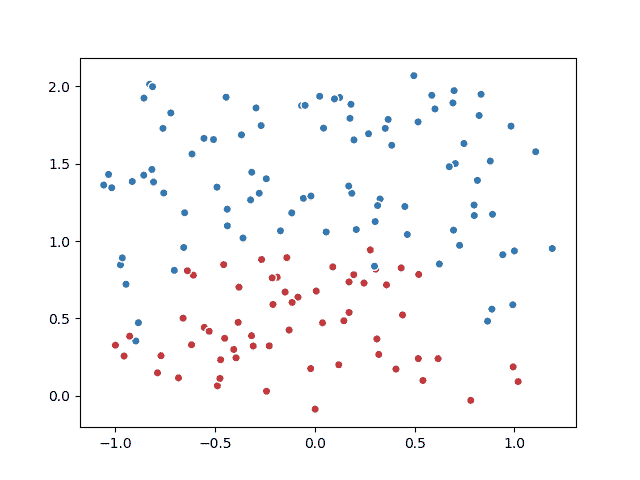
- 训练不带正则项的损失函数mse_loss,可以看到有严重的过拟合现象:
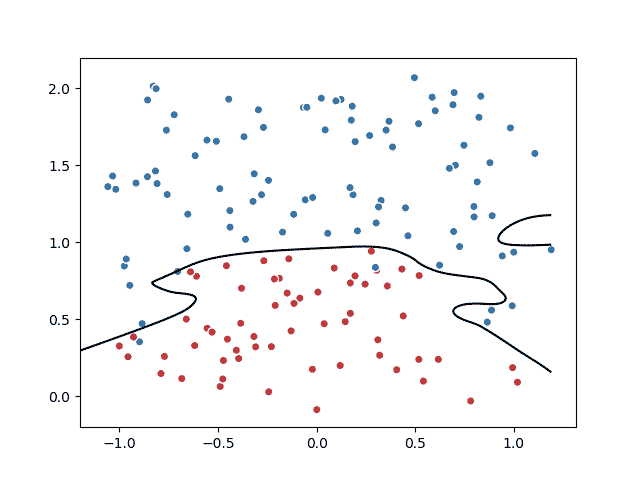
- 训练带正则项的损失函数loss,解决了前面的过拟合问题:
如果想通过实战来加深理解损失函数、学习率、滑动平均等,可以参考这些深层神经网络和优化算法的小DEMO